10405. Наибольшая общая подпоследовательность

По заданным двум символьным последовательностям найти длину наибольшей общей подпоследовательности. Например, длина наибольшей общей подпоследовательности последовательностей abcdgh и aedfhr равна 3.

Вход. Состоит из пар строк. Первая строка содержит первую последовательность, а вторая строка – вторую последовательность. Каждая входная последовательность содержит не более 1000 символов.

Выход. Для каждого теста вывести в отдельной строке длину наибольшей общей подпоследовательности.

Пример входа

a1b2c3d4e
zz1yy2xx3ww4vv
abcdgh
aedfhr
abcdefghijklmnopqrstuvwxyz
a0b0c0d0e0f0g0h0i0j0k0l0m0n0o0p0q0r0s0t0u0v0w0x0y0z0
abcdefghijklmnzyxwvutsrqpo
opqrstuvwxyzabcdefghijklmn

Пример выхода

4
3
26
14

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Пусть f(i, j) – длина наибольшей общей подпоследовательности (НОП) последовательностей x₁x₂…x_i и y₁y₂…y_j.

Если x_i ¹ y_j, то ищем НОП среди x₁x₂…x_i-1 и y₁y₂…y_j, а также среди x₁x₂…x_i и y₁y₂…y_j-1. Большую из них возвращаем:

f(i, j) = max( f(i, j – 1), f(i – 1, j) )

Если x_i = y_j, то ищем НОП среди x₁x₂…x_i-1 и y₁y₂…y_j-1:

f(i, j) = 1 + f(i – 1, j – 1)

Значения f(i, j) будем хранить в массиве m[0..1000, 0..1000], где m[0][i] = m[i][0] = 0.

Каждая следующая строка массива m[i][j] вычисляется через предыдущую. Поэтому для нахождения ответа достаточно держать в памяти только две строки длины 1000.

Пример

Пусть X = abcdgh, Y = aedfhr. Наибольшей общей подпоследовательностью будет adh, ее длина равна f(6, 6) = 3.

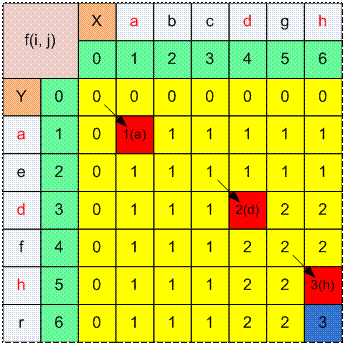
f(6, 6) = max(f(6, 5), f(5, 6)) = max(2, 3) = 3, так как Y[6] = r ≠ h = X[6].

f(5, 6) = 1 + f(4, 5) = 1 + 2 = 3, так как Y[5] = h = X[6].

Реализация алгоритма

Определим функцию max, вычисляющую максимум двух чисел:

int max(int i,int j)

{

return (i > j) ? i : j;

}

Массивы x и y содержат входные последовательности, lenx и leny – их длины. Массив m содержит две последние строки динамического преобразования.

char x[1001], y[1001];

int m[2][1001];

int lenx, leny;

Входные данные обрабатываем, пока не встретится конец файла. Читаем две входные последовательности в массивы x и y. При этом значения x[0] и y[0] обнуляем, а входные строки заносим в массивы, начиная с первой ячейки. Длины последовательностей сохраняем в переменных lenx и leny.

x[0] = y[0] = 0;

while(gets(x+1),gets(y+1))

{

lenx = strlen(x+1); leny = strlen(y+1);

Обнуляем массив m. Динамически вычисляем значения f(i, j). Изначально m[0][j] содержит значения f(0, j). Далее в m[1][j] заносим значения f(1, j). Поскольку для вычисления f(2, j) достаточно иметь значения двух предыдущих строк массива m, то значения f(2, j) можно сохранять в ячейках m[0][j], значения f(3, j) – в ячейках m[1][j] и так далее.

memset(m,0,sizeof(m));

for(i = 1; i <= lenx; i++)

for(j = 1; j <= leny; j++)

if (x[i] == y[j]) m[i % 2][j] = 1 + m[(i-1)%2][j-1];

else m[i % 2][j] = max(m[(i-1)%2][j],m[i%2][j-1]);

В конце алгоритма длина наибольшей общей подпоследовательности будет находиться в ячейке m[lenx%2][leny]. Выводим ее.

printf("%d\n",m[lenx%2][leny]);

}